Logic & Structure

Logic & Structure—the current online project—is an experiment in merging the formal language of mathematical logic with a visual arts practice.

The project began in 2015 with a challenge from a mathematician who asked his artist friends whether the rules of mathematical logic could be applied when creating a work of art. The question remains open, but the artists’ responses to the challenge resulted in three group shows. The first two were hosted by The Painters Gallery (2015, 2017), the last one took place in March 2024 at ArtUp Gallery in Margaretville, NY.

Over the last few years, several discussions, email exchanges, and informal workshops have taken place. The 2024 online workshop is intended for artists interested in exploring a variety of related ideas.

Mathematical Logic for Visual Artists—A Workshop

In everyday language the word structure is understood as something of many parts that is put together. Structure comes from the Latin word structura meaning “a fitting together, building,” which suggests that the way the parts are assembled ensures the stability and durability of the whole.

In this project, which introduces the language of mathematical logic into the domain of visual arts, the meaning of the word is different. Structure is a collection of arbitrarily chosen elements—a set—and what binds them—relations—can be almost anything that comes to mind. The elements don’t have to be physically “put together” if we know how to locate them and are able to tell if one is related to another according to the chosen criteria.

In the example below, the elements of the set are all conveniently located on a table, which constitutes a domain of a structure.

In the example below, the elements of the set are all gathered under one roof. The gallery space becomes the domain of the structure.

The two different sets of elements shown above, can be called structures if we manage to define them as such.

Here is the formal definition: A structure is a set with a set of relations on it.

The concept is abstract and open to interpretations, but at the same time, the procedure for creating a structure is simple and exact: one must define elements of a set and relations between them. To do that, we need a verbal counterpart of a visual piece — a concise description. While describing elements and relations, one can always say too much or too little, this is why “logic” comes first in the workshop title. It provides the tools for describing more by saying less.

To master the art of concise description it is helpful to get familiar with the concept of unary and binary relations.

PART I: UNARY RELATIONS

A relation is unary if you don’t need to compare the element with any other in the set to be able to decide whether the element has a given property, for example: to be yellow, round, or in the upper left corner on a page. In other words: being yellow is self-evident unlike being similar, smaller, or further in line.

The properties of single elements are not really relations in the common understanding of the word, but in mathematical logic they are called relations for uniformity of terminology: there are unary relations, binary, ternary, quaternary, and so on.

Following the claim that a structure can be anything, here is a photo depicting 15 toy figurines.

Depending on our choice of unary relations, we can distinguish within this set of 15 elements several subsets. The descriptions can be brief. For example, “fallen.” This choice suggests that some figurines might be fallen and some other might be not—they are “standing.”  Similarly, the property defined as “having all body parts” suggests that some figurines in the set might have a leg or a head missing. “Being a human” suggests that there are other elements—a horse in this case. (It is not required that the set contains an element other than the defined one. If there are no figurines other than “fallen” in the set, it is still formally a structure.)

Some elements might have more than one property. A photo below shows an element that has two properties: “fallen” and “armed.” Such a case of overlapping sets has been popularized by the Venn diagram, which consists of overlapping circles indicating which properties are shared.

The Venn diagram-style circles are superimposed on the photo above to indicate an overlap of the set of “armed” figurines and the set of “fallen,” and to exclude “not armed, not fallen.”

While the Venn diagram is ubiquitous and pops up on the Internet in various contexts, Boolean combinations are less known. Learning what they are gives an insight into the power of logic: how from very little one can build a lot. With just two distinct properties that can overlap and three logical connectives (AND, OR, and NOT) one can build 16 different configurations. It seems like a lot, but even more surprisingly three distinct overlapping properties give 256 combinations. Moreover, the numbers 16 and 256 are optimal.

INSTRUCTIONS FOR PART I OF THE WORKSHOP: The illustration below has two parts. The box on the left is a Venn Diagram showing all the different Boolean combinations of two distinct unary relations, called here R and S. The 16 boxes on the right show all 16 configurations mentioned above. Use the boxes on the right as a guide for creating an artwork.

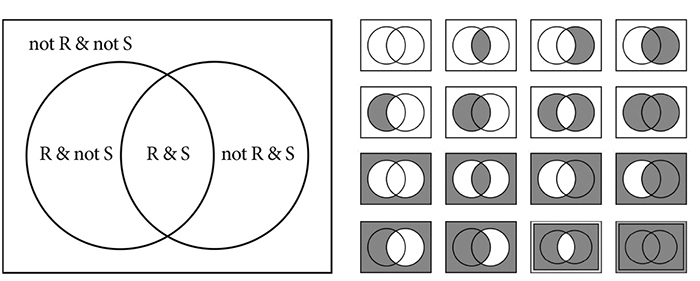
The artwork should consist of 16 pieces. In each, identify elements having some property R and elements having some property S. Choose the properties so that some of the elements can have both properties and some can have none. There will be extreme cases. For example, in the work representing the first empty box, each element has neither R nor S property. In the work for the last box, there must be elements having all 4 combinations of the properties, as in the Venn diagram on the left.

PART II: BINARY RELATIONS

Binary relation is a relation that requires compering pairs of elements of a set: to be brighter, lighter, higher, broader, etc. To keep track of the binary relations one can make a list of related pairs, or, more conveniently, represent elements as dots and connect them with lines. Such a graph illustrating relations is a bit like an X-ray. It gives an insight into what hides under the surface.

In a graph, to indicate which element is bigger or heavier, or brighter, a connecting line ends with an arrow. If a relation is symmetrical like “being of a different size” or “similar,” no arrow is needed.

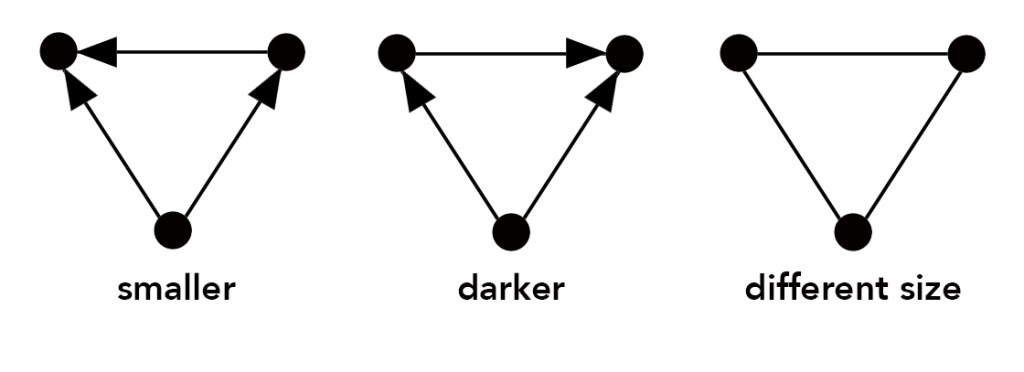
There are many kinds of relations to consider while examining a single structure, seeing them depends on ingenuity and imagination. Some relations that come to mind turn out to be perfunctory, trivial, irrelevant, some reveal the gist of the structure, or something surprising about it. Examining binary relations allows you to see the features of the structure that can be easily missed, one of them is symmetry hiding in the nooks and crannies of an intricate set of relations. Sometimes symmetry is hard to notice even if the set of relations is small.

Again, the word symmetry can be misleading because in the language of everyday life it is understood as a mirror image in which all elements are repeated in a reflection. This term used in the context of mathematical structure has more nuanced meaning: there might be only some elements in a structure, not all, which can be swapped without changing anything in the hierarchy of the binary relations order. The following comparison might give an idea: if the forking roads lead to the same spot, then deciding which way to turn is not an issue for a driver.

INSTRUCTIONS FOR PART II OF THE WORKSHOP: Create a two-dimensional artwork and identify the elements and one binary relation in it. Draw the graph of this relation as described above. Try to make it so that the graph is a bit complicated. See what the graph would look like in three dimensions, for example as connected wires. Create an artwork with hardly noticeable symmetry or symmetries.

PART III: ISOMORPHISM

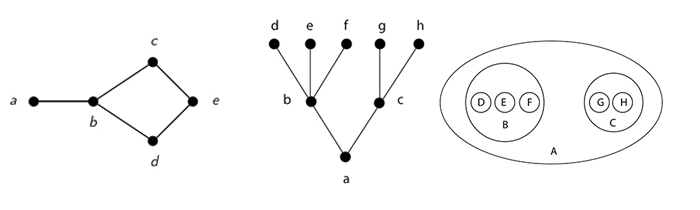
A set, as we know, can be anything. It could be a list of female monarchs of England, or a list of American submarines used in combat during the World War II. If it happens that the number of English queens and American submarines is the same, then it is legitimate to compare these two sets. If binary relations “longer in service” and “larger” pair the elements the same way in both sets, then it is legitimate to say that the two structures are the same. With over 200 U.S. submarines in combat during the World War II the comparison is not possible. A set of Polish submarines (five) and female monarchs of Netherlands (four) doesn’t meet the criteria either; the number must be exact. Counting the number of elements seems limiting, but it never limited great poets whose verses and stanzas followed a certain numerical pattern; besides, an element of a structure doesn’t have to be a circle or a square, it can be a bouquet—a cluster of elements.

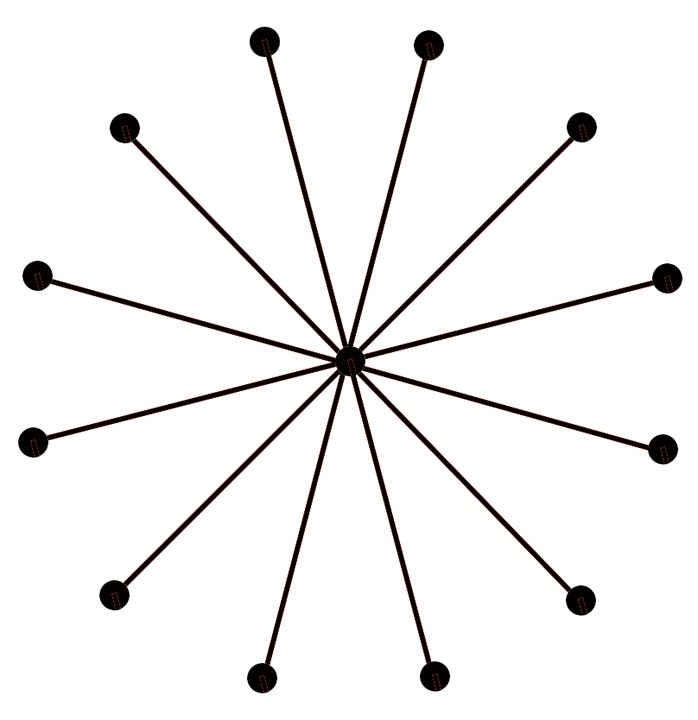
Below is an example of two structures that are isomorphic. Each structure has 13 elements, and the relation is “different size.” In the drawing on the left, 12 same size elements are related to a bigger one, in the drawing on the right, 12 same size elements are related to a smaller one. A graph illustrating these relations will be the same.

The diagram below illustrates to what extent appearances are deceiving: these two different looking graphs are isomorphic.

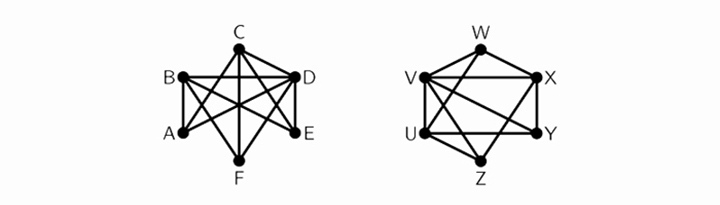
The graph on the left can be redrawn to look like the one on the right as follows:
A⟷W, E⟷Y, F⟷Z, B⟷U, C⟷X, D⟷V

INSTRUCTIONS FOR PART III OF THE WORKSHOP: Create two isomorphic structures that have a distinctly different look.